卡尔曼滤波器:递归算法

丁毅桂2025/1/5大约 2 分钟

卡尔曼滤波器学习笔记

【卡尔曼滤波器】_DR_CAN合集学习笔记

卡尔曼滤波器(Kalman Filter)

不是一般意义上的滤波器
是一种最优化递归数字处理算法(optimal recursive data processing algorithm)
更像是一种观测器(observer)

卡尔曼滤波器广泛应用的原因：世界中存在大量不确定性

不存在完美的数学模型
系统的扰动不可控，难以建模
测量的传感器存在误差

递归算法

案例：

用尺子多次测量硬币的直径 $Z$ ，
使用求平均数的方式估计硬币真实直径 $\hat{X}$ 。

测量结果

第n次测量结果 $Z_{n}$
$Z_{1} = 50.1 m m$
$Z_{2} = 50.4 m m$
$Z_{2} = 50.2 m m$

求平均数公式推导递归算法：

\begin{aligned} {\hat{X}}_{n} & = \frac{1}{n} (Z_{1} + Z_{2} + \dots + Z_{n}) \\ = \frac{1}{n} (Z_{1} + Z_{2} + \dots + Z_{n - 1}) + \frac{1}{n} Z_{n} \\ = \frac{n - 1}{n} \frac{1}{n - 1} (Z_{1} + Z_{2} + \dots + Z_{n - 1}) + \frac{1}{n} Z_{n} \\ = \frac{n - 1}{n} {\hat{X}}_{n - 1} + \frac{1}{n} Z_{n} \\ = {\hat{X}}_{n - 1} - \frac{1}{n} {\hat{X}}_{n - 1} + \frac{1}{n} Z_{n} \\ = {\hat{X}}_{n - 1} - \frac{1}{n} (Z_{n} - {\hat{X}}_{n - 1}) \end{aligned}

结论

{\hat{X}}_{n} = {\hat{X}}_{n - 1} - \frac{1}{n} (Z_{n} - {\hat{X}}_{n - 1}) 本次估计 = 上次估计 + \frac{1}{n} (本次测量 - 上次估计)

n \to + \infty; \frac{1}{n} \to 0; {\hat{X}}_{n} \to {\hat{X}}_{n - 1}; 随着测量次数增加；测量结果不再重要；估计值逐渐稳定； n \to 0; \frac{1}{n} \to + \infty; {\hat{X}}_{n} \to Z_{n}; 测量次数较小时；测量结果作用较大；估计值受测量结果影响较大；

卡尔曼增益K

把上面案例中的系数 $\frac{1}{n}$ 换成代表卡尔曼增益的系数K,

那么就得到了卡尔曼滤波算法中的第一个公式：

{\hat{X}}_{n} = {\hat{X}}_{n - 1} + K_{n} (Z_{n} - {\hat{X}}_{n - 1}) 本次估计 = 上次估计 + 增益系数K (本次测量 - 上次估计)

其中卡尔曼增益K

K_{n} = \frac{e_{E S T_{n - 1}}}{e_{E S T_{n - 1}} + e_{M E A_{n}}} 本次卡尔纳曼增益 = \frac{上次估计误差}{上次估计误差+本次测量误差}

分析：

$估计误差 ≫ 测量误差; K \to 1; 本次估计 \to 本次测量;$
$估计误差 ≪ 测量误差; K \to 0; 本次估计 \to 上次估计;$

卡尔曼滤波计算三步骤

第一步:计算卡尔曼增益

K_{n} = \frac{e_{E S T_{n - 1}}}{e_{E S T_{n - 1}} + e_{M E A_{n}}}

第二步：计算估计值

{\hat{X}}_{n} = {\hat{X}}_{n - 1} + K_{n} (Z_{n} - {\hat{X}}_{n - 1})

第三步：更新估计误差

e_{E S T_{n}} = (1 - K_{n}) e_{E S T_{n - 1}}

案例

import numpy as np
import matplotlib.pyplot as plt

# 数据

N = 50
Z = []
X = [0] # 估计值初值0

Error_mes = 5 # 测量误差
Error_est = 50 # 估计误差 初值50mm
K = 0 # 卡尔曼增益

# 生成随机数据： 均值 50mm 测量误差 5mm
for i in range(0,N):
    Z.append(np.random.normal(50,5)) 

for i in range(1,N):
    K = Error_est/(Error_est+Error_mes) # 卡尔曼增益=估计误差/（估计误差+测量误差）
    x = X[i-1] + K * (Z[i] - X[i-1]) # 估计值=测量值-K*(测量值-真实值)
    Error_est = (1-K) * Error_est # 估计误差=（1-K）*估计误差
    X.append(x)


# 绘制图形
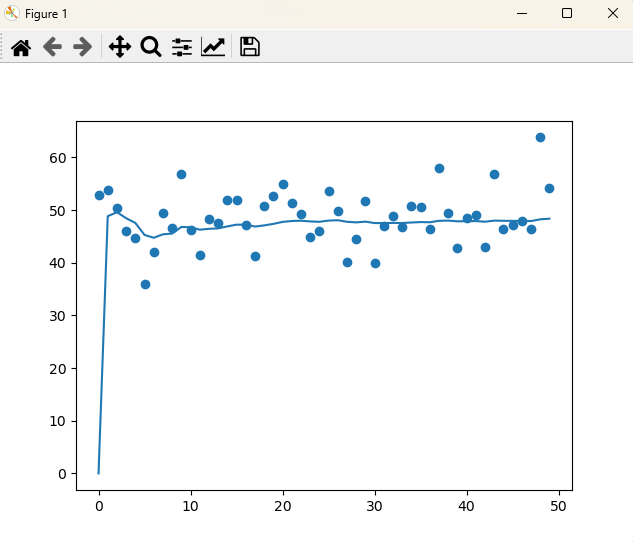
plt.scatter(range(0,len(Z)),Z) # 点图 测量值
plt.plot(range(0,len(X)),X)  # 折线图 估计值
# 显示图形
plt.show()

alt text