卡尔曼滤波器:协方差矩阵

卡尔曼滤波器学习笔记

【卡尔曼滤波器】_DR_CAN合集学习笔记

协方差矩阵（Covariance Matrix）

方差

• 定义：方差衡量数据相对于均值的离散程度，是统计学中描述数据波动大小的重要指标。
• 计算公式：$$\text{Var}(X)=\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2$$其中，$X$ 是随机变量，$x_i$ 是数据点，$\mu$ 是均值，$n$ 是数据点的数量。
• 说明:
  • 方差计算的是各个数据点与均值之差的平方的平均值。
  • 方差值越大，表示数据点越分散；
  • 方差值越小，表示数据点越集中.

协方差

• 定义：协方差是衡量两个随机变量之间线性相关程度的统计量.
• 计算公式：$$\text{Cov}(X,Y)=\frac{1}{n}\sum _{i=1}^n(x_i-{\mu }_X)(y_i-{\mu }_Y)$$其中，$X$ 和 $Y$ 是两个随机变量，$x_i$ 和 $y_i$ 分别是 $X$ 和 $Y$ 的数据点，${\mu }_X$ 和 ${\mu }_Y$ 分别是 $X$ 和 $Y$ 的均值，$n$ 是数据点的数量.
• 相关性体现：
  • 当 $(x_i-{\mu }_X)(y_i-{\mu }_Y)$ 为同号相乘（即 $x_i$ 和 $y_i$ 同时高于或低于各自均值），乘积为正，累加后为正，体现正相关.
  • 当 $(x_i-{\mu }_X)(y_i-{\mu }_Y)$ 为异号相乘（即 $x_i$ 高于均值而 $y_i$ 低于均值，或反之），乘积为负，累加后为负，体现负相关.
• 协方差取值含义：
  • 如果协方差为正，表示两个变量正相关；
  • 如果协方差为负，表示两个变量负相关；
  • 如果协方差为零，表示两个变量不相关

协方差矩阵

• 将方差和协方差写在一个矩阵中,体现变量间的联动关系:离散程度和相关性.
• 计算公式:$$\begin{array}{rl}\mathbf{\Sigma }(X,Y,Z)& =\left[\begin{array}{ccc}\text{Cov}(X,X)& \text{Cov}(X,Y)& \text{Cov}(X,Z)\\ \text{Cov}(Y,X)& \text{Cov}(Y,Y)& \text{Cov}(Y,Z)\\ \text{Cov}(Z,X)& \text{Cov}(Z,Y)& \text{Cov}(Z,Z)\end{array}\right]\\ & =\left[\begin{array}{ccc}\text{Var}(X)& \text{Cov}(X,Y)& \text{Cov}(X,Z)\\ \text{Cov}(Y,X)& \text{Var}(Y)& \text{Cov}(Y,Z)\\ \text{Cov}(Z,X)& \text{Cov}(Z,Y)& \text{Var}(Z)\end{array}\right]\end{array}$$
• 主对角线上元素体现的是随机变量的方差，非对角线上元素体现的是两个随机变量之间的协方差。
• 构造过度矩阵A:$$\begin{array}{rlr}A(X,Y,Z)& =\left[\begin{array}{ccc}{x}_1-\overline{x}& y_1-\overline{y}& z_1-\overline{z}\\ x_2-\overline{x}& y_2-\overline{y}& z_2-\overline{z}\\ x_3-\overline{x}& y_3-\overline{y}& z_3-\overline{z}\end{array}\right]& \text{(各个元素和均值的偏差)}\\ & =\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right]-\left[\begin{array}{ccc}\overline{x}& \overline{y}& \overline{z}\\ \overline{x}& \overline{y}& \overline{z}\\ \overline{x}& \overline{y}& \overline{z}\end{array}\right]\\ & =\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right]-\frac{1}{3}\left[\begin{array}{ccc}{x}_1+x_2+x_3& y_1+y_2+y_3& z_1+z_2+z_3\\ x_1+x_2+x_3& y_1+y_2+y_3& z_1+z_2+z_3\\ x_1+x_2+x_3& y_1+y_2+y_3& z_1+z_2+z_3\end{array}\right]\\ & =\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right]-\frac{1}{3}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right]\end{array}$$
• 通过过渡矩阵A求协方差矩阵:$$\begin{array}{rl}\mathbf{\Sigma }(X,Y,Z)& =\left[\begin{array}{ccc}\text{Cov}(X,X)& \text{Cov}(X,Y)& \text{Cov}(X,Z)\\ \text{Cov}(Y,X)& \text{Cov}(Y,Y)& \text{Cov}(Y,Z)\\ \text{Cov}(Z,X)& \text{Cov}(Z,Y)& \text{Cov}(Z,Z)\end{array}\right]\\ & =\left[\begin{array}{ccc}\frac{1}{n}\sum _{i=1}^n(x_i-\overline{X})(x_i-\overline{X})& \frac{1}{n}\sum _{i=1}^n(x_i-\overline{X})(y_i-\overline{Y})& \frac{1}{n}\sum _{i=1}^n(x_i-\overline{X})(z_i-\overline{Z})\\ \frac{1}{n}\sum _{i=1}^n(y_i-\overline{Y})(x_i-\overline{X})& \frac{1}{n}\sum _{i=1}^n(y_i-\overline{Y})(y_i-\overline{Y})& \frac{1}{n}\sum _{i=1}^n(y_i-\overline{Y})(z_i-\overline{Z})\\ \frac{1}{n}\sum _{i=1}^n(z_i-\overline{Z})(x_i-\overline{X})& \frac{1}{n}\sum _{i=1}^n(z_i-\overline{Z})(y_i-\overline{Y})& \frac{1}{n}\sum _{i=1}^n(z_i-\overline{Z})(z_i-\overline{Z})\end{array}\right]\\ & =\frac{1}{3}\left[\begin{array}{ccc}{x}_1-\overline{x}& x_2-\overline{x}& x_3-\overline{x}\\ y_1-\overline{y}& y_2-\overline{y}& y_3-\overline{y}\\ z_1-\overline{z}& z_2-\overline{z}& z_3-\overline{z}\end{array}\right]\left[\begin{array}{ccc}{x}_1-\overline{x}& y_1-\overline{y}& z_1-\overline{z}\\ x_2-\overline{x}& y_2-\overline{y}& z_2-\overline{z}\\ x_3-\overline{x}& y_3-\overline{y}& z_3-\overline{z}\end{array}\right]\\ & =\frac{1}{3}{A}^{T}A\end{array}$$

案例

import numpy as np
print(np.__version__) # 2.1.3

#####################################################################################
####################################### 方法1 #######################################
#####################################################################################
# 协方差
def covariance(x, y):
    x_mean = np.mean(x)
    y_mean = np.mean(y)
    return np.sum((x-x_mean)*(y-y_mean))/(len(x))

# 协方差矩阵
def covariance_matrix1(x, y, z):
    return np.matrix([[covariance(x, x), covariance(x, y), covariance(x, z)],
                      [covariance(y, x), covariance(y, y), covariance(y, z)],
                      [covariance(z, x), covariance(z, y), covariance(z, z)]])


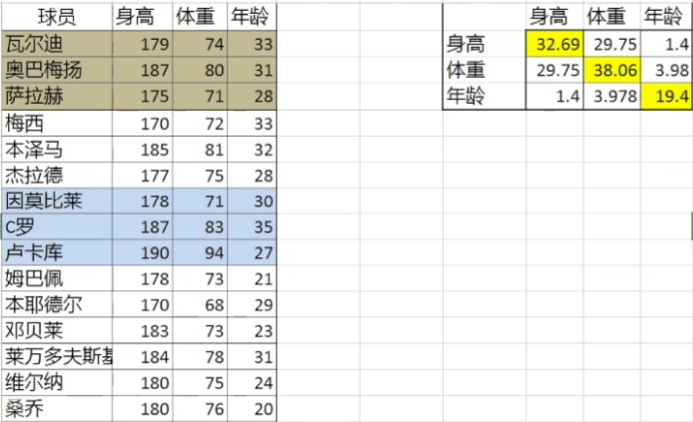
height = [179,187,175,170,185,177,178,187,190,178,170,183,184,180,180]
weight = [74,80,71,72,81,75,71,83,94,73,68,73,78,75,76]
age = [33,31,28,33,32,28,30,35,27,21,29,23,31,24,20]

print(covariance_matrix1(height, weight, age))
"""
输出:
[[32.69333333 29.74666667  1.4       ]
 [29.74666667 38.06222222  3.97777778]
 [ 1.4         3.97777778 19.42222222]]
"""

#####################################################################################
####################################### 方法2 #######################################
#####################################################################################
# 计算过渡矩阵
def A(x,y,z):
    m = np.matrix([x,y,z]).T
    return m - np.mean(m, axis=0) # axis=0 表示沿着矩阵的列方向计算均值，即对每一列的所有元素求平均值。

# 利用过渡矩阵计算协方差矩阵
def covariance_matrix2(x, y, z):
    a = A(x,y,z)
    return np.dot(a.T, a)/len(x)

print(covariance_matrix2(height, weight, age))
"""
输出:
[[32.69333333 29.74666667  1.4       ]
 [29.74666667 38.06222222  3.97777778]
 [ 1.4         3.97777778 19.42222222]]
"""