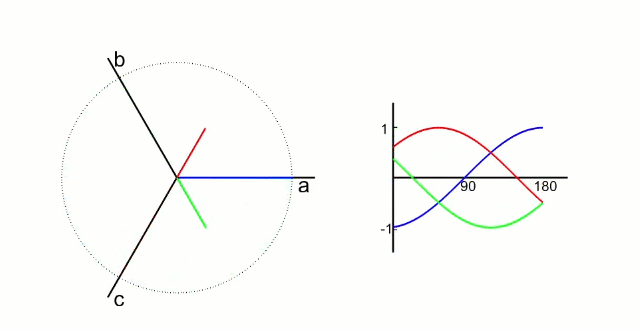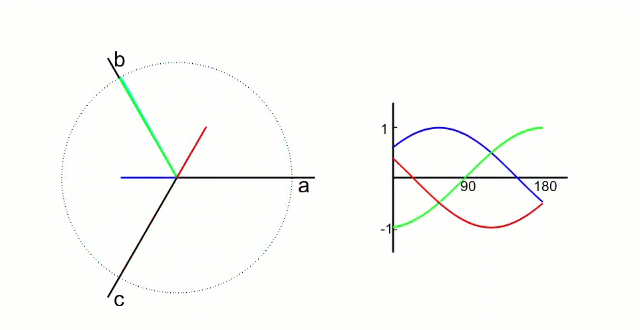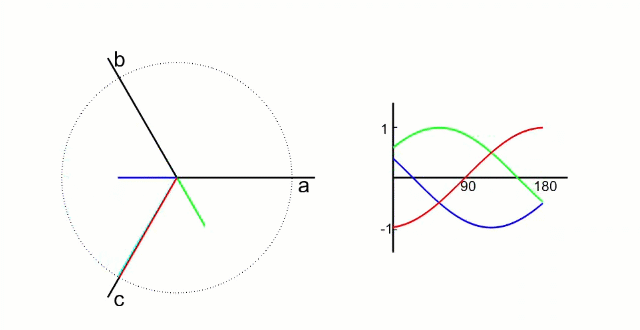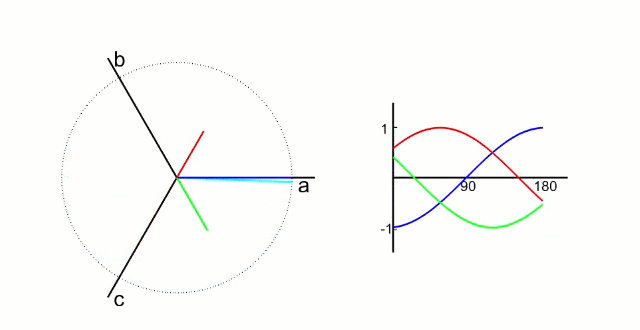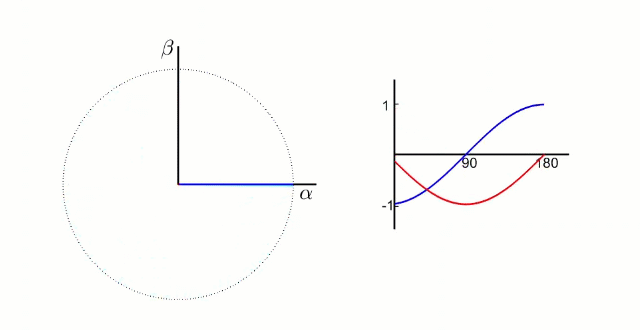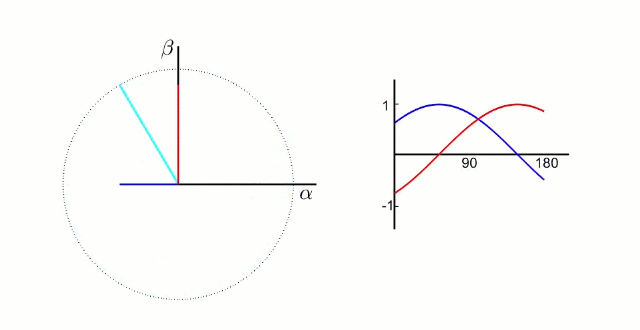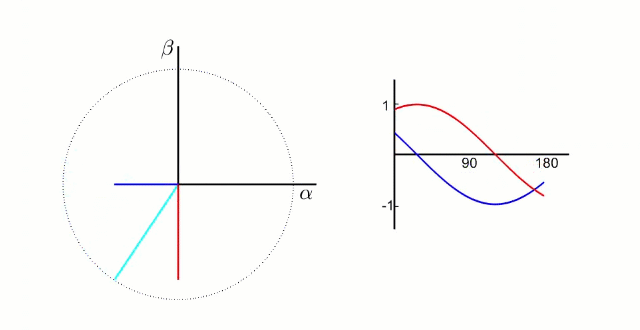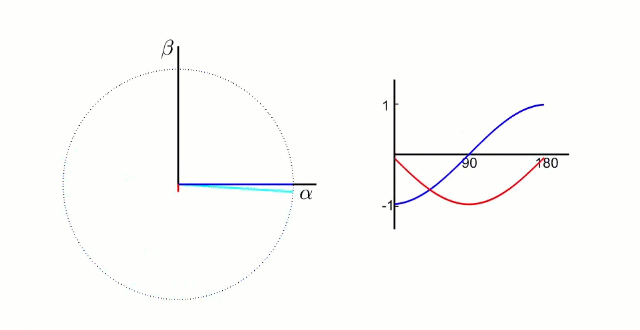FOC算法学习与实现笔记-01.克拉克变换

克拉克变换

实际上，完成克拉克变换后得到的α和β值，描述的是电机定子内的磁场（力矩和方向）

• 克拉克变换就是把相位差为120度的三相电映射到二维平面上。
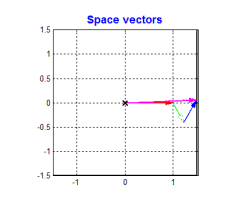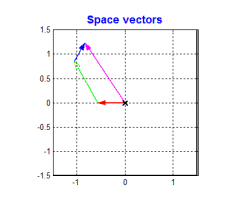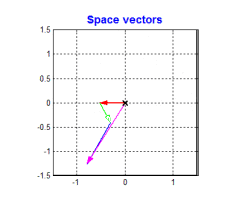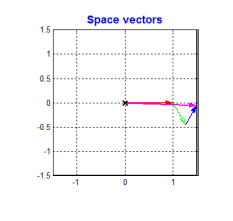
• 具体做法就是把三相电看成三个矢量（也反映了三个方向的磁场强度）
• 把三个矢量相加得到一个矢量（也反应了定子产生磁场的方向和强度）
• 这个矢量只需要用两个量（α、β）来表示。

电机内三相电的波形和磁场方向

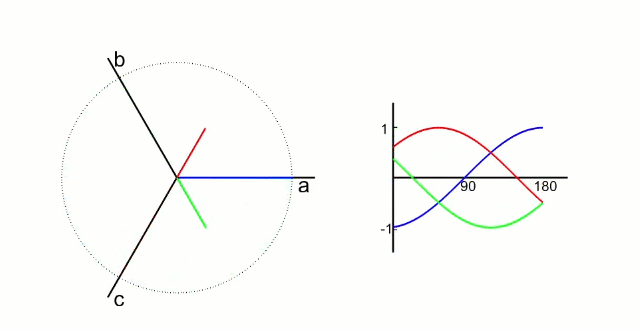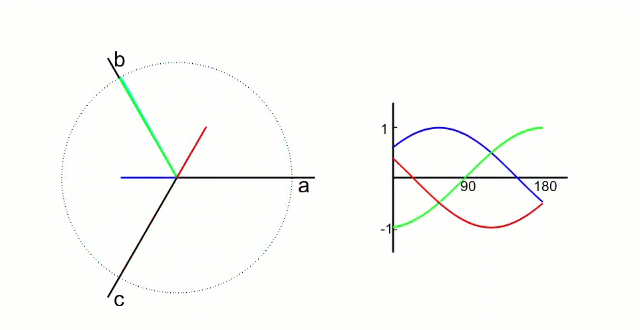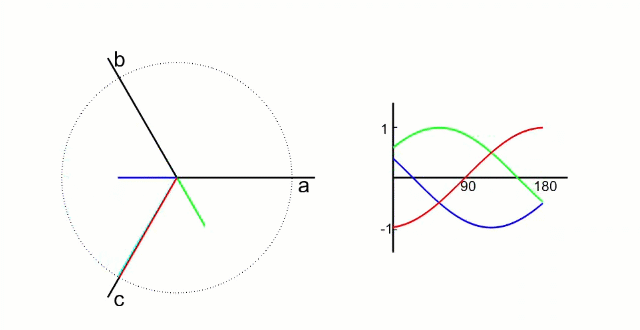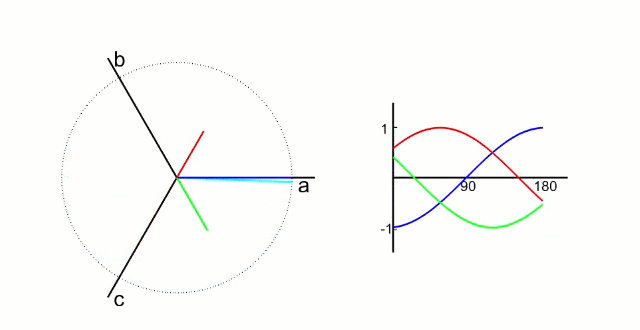
克拉克变换后电机，α和β的波形和磁场方向

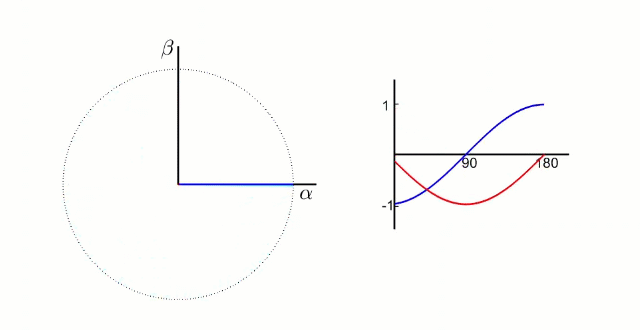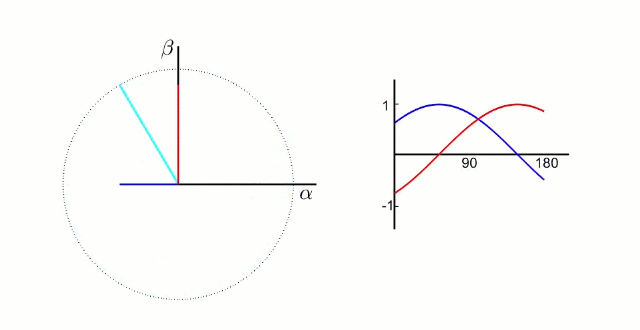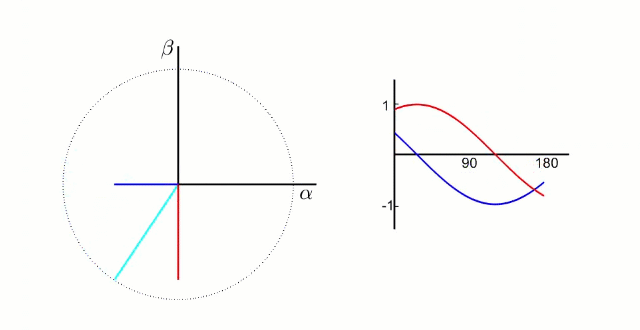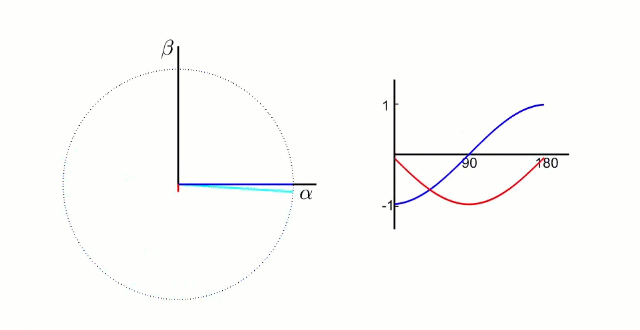
克拉克变换的本质就是把三个矢量相加

基本形式

基本形式的推导

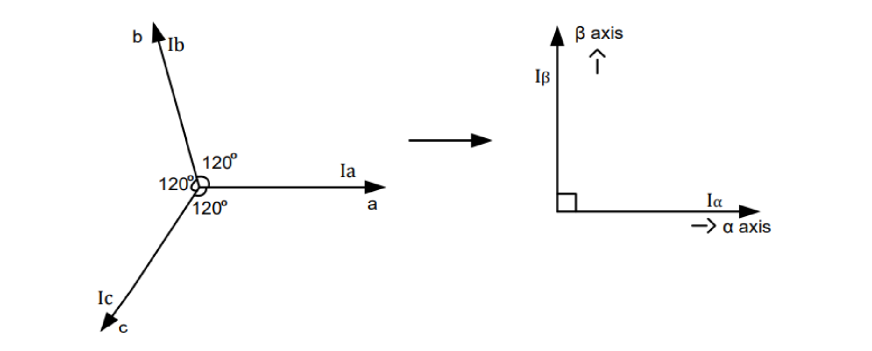
• 这个推导过程很简单
• 就是分别计算三个分量作用在α轴、β轴上的值。
• 如
  • ia
    • 作用在α轴上 $I_{\alpha }=\cos 0\ast i_a$
    • 作用在β轴上 $I_{\beta }=\sin 0\ast i_a$
  • ib
    • 作用在α轴上 $I_{\alpha }=\cos 120\ast i_b$
    • 作用在β轴上 $I_{\beta }=\sin 120\ast i_b$
  • ic
    • 作用在α轴上 $I_{\alpha }=\cos -120\ast i_c$
    • 作用在β轴上 $I_{\beta }=\sin -120\ast i_c$

代数形式：

$$\begin{gathered} I_{\alpha }=\cos 0\mathrm{°}\ast i_a+\cos 120\mathrm{°}\ast i_b+\cos 240\mathrm{°}\ast i_c \\ {I}_{\beta }=\sin 0\mathrm{°}\ast i_a+\sin 120\mathrm{°}\ast i_b+\sin 240\mathrm{°}\ast i_c \end{gathered}$$

矩阵形式为：

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{ccc}\cos 0\mathrm{°}& \cos 120\mathrm{°}& \cos 240\mathrm{°}\\ \sin 0\mathrm{°}& \sin 120\mathrm{°}& \sin 240\mathrm{°}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$$

上面这里特意写成三角函数，因为感觉形式比较优美

简化后的矩阵形式为：

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$$

基本形式的化简

还可以利用基尔霍夫电流定律进一步化简：

$$\begin{gathered} i_a+i_b+i_c=0 \\ {i}_c=-(i_a+i_b) \end{gathered}$$

变换矩阵

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{ccc}\cos 0\mathrm{°}& \cos 120\mathrm{°}& \cos 240\mathrm{°}\\ \sin 0\mathrm{°}& \sin 120\mathrm{°}& \sin 240\mathrm{°}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ -(i_a+i_b)\end{array}\right]$$

展开计算

$$\begin{gathered} I_{\alpha }=\cos 0\mathrm{°}\ast i_a+\cos 120\mathrm{°}\ast i_b+\cos 240\mathrm{°}\ast -(i_a+i_b) \\ {I}_{\beta }=\sin 0\mathrm{°}\ast i_a+\sin 120\mathrm{°}\ast i_b+\sin 240\mathrm{°}\ast -(i_a+i_b) \end{gathered}$$

简化计算

$$\begin{gathered} I_{\alpha }=(\cos 0\mathrm{°}-\cos 240\mathrm{°})\ast i_a+(\cos 120\mathrm{°}-\cos 240\mathrm{°})\ast i_b \\ {I}_{\beta }=(\sin 0\mathrm{°}-\sin 240\mathrm{°})\ast i_a+(\sin 120\mathrm{°}-\sin 240\mathrm{°})\ast i_b \end{gathered}$$

最终矩阵形式：

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{cc}(\cos 0\mathrm{°}-\cos 240\mathrm{°})& (\cos 120\mathrm{°}-\cos 240\mathrm{°})\\ (\sin 0\mathrm{°}-\sin 240\mathrm{°})& (\sin 120\mathrm{°}-\sin 240\mathrm{°})\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\end{array}\right]$$

三角函数计算：

• $\cos 0^{\circ }=1$
• $\cos {120}^{\circ }=-\frac{1}{2}$
• $\cos {240}^{\circ }=-\frac{1}{2}$
• $\sin 0^{\circ }=0$
• $\sin {120}^{\circ }=\frac{\sqrt{3}}{2}$
• $\sin {240}^{\circ }=-\frac{\sqrt{3}}{2}$

因此，

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{cc}(1+\frac{1}{2})& (-\frac{1}{2}+\frac{1}{2})\\ (0+\frac{\sqrt{3}}{2})& (\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2})\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\end{array}\right]$$

简化后得到：

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\left[\begin{array}{cc}\frac{3}{2}& 0\\ \frac{\sqrt{3}}{2}& \sqrt{3}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\end{array}\right]$$

基本形式的逆变换

为了找到给定矩阵的逆矩阵，我们首先需要计算原始矩阵。给定的矩阵为:

$$\mathbf{A}=\left[\begin{array}{cc}\frac{3}{2}& 0\\ \frac{\sqrt{3}}{2}& \sqrt{3}\end{array}\right]$$

接下来，我们需要找到这个矩阵的逆矩阵。对于一个2x2矩阵 $\mathbf{A}=\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$，其逆矩阵 ${\mathbf{A}}^{-1}$ 可以通过以下公式计算:

$${\mathbf{A}}^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]$$

因此, 对于我们的矩阵 $\mathbf{A}$:

$${\mathbf{A}}^{-1}=\frac{1}{\left(\frac{3}{2}\right)\left(\sqrt{3}\right)-\left(\frac{\sqrt{3}}{2}\right)\left(0\right)}\left[\begin{array}{cc}\sqrt{3}& 0\\ -\frac{\sqrt{3}}{2}& \frac{3}{2}\end{array}\right]$$$${\mathbf{A}}^{-1}=\frac{1}{\frac{3\sqrt{3}}{2}}\left[\begin{array}{cc}\sqrt{3}& 0\\ -\frac{\sqrt{3}}{2}& \frac{3}{2}\end{array}\right]$$$${\mathbf{A}}^{-1}=\frac{2}{3\sqrt{3}}\left[\begin{array}{cc}\sqrt{3}& 0\\ -\frac{\sqrt{3}}{2}& \frac{3}{2}\end{array}\right]$$$${\mathbf{A}}^{-1}=\frac{2}{3\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}\left[\begin{array}{cc}\sqrt{3}& 0\\ -\frac{\sqrt{3}}{2}& \frac{3}{2}\end{array}\right]$$$${\mathbf{A}}^{-1}=\frac{2}{3\cdot 3}\left[\begin{array}{cc}3& 0\\ -\frac{3}{2}& \frac{3\sqrt{3}}{2}\end{array}\right]$$$${\mathbf{A}}^{-1}=\frac{2}{9}\left[\begin{array}{cc}3& 0\\ -\frac{3}{2}& \frac{3\sqrt{3}}{2}\end{array}\right]$$$${\mathbf{A}}^{-1}=\left[\begin{array}{cc}\frac{2}{3}& 0\\ -\frac{1}{3}& \frac{\sqrt{3}}{3}\end{array}\right]$$

因此, 原始矩阵的逆矩阵为:

$${\mathbf{A}}^{-1}=\left[\begin{array}{cc}\frac{2}{3}& 0\\ -\frac{1}{3}& \frac{\sqrt{3}}{3}\end{array}\right]$$

因此, 基本形式的逆变换为:

$$\begin{array}{rl}\left[\begin{array}{c}{i}_a\\ i_b\end{array}\right]& =\left[\begin{array}{cc}\frac{2}{3}& 0\\ -\frac{1}{3}& \frac{\sqrt{3}}{3}\end{array}\right]\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]\\ i_c& =-(i_a+i_b)\end{array}$$

等幅值形式

等幅值形式的推导

• 简单来说，就是添加了一个系数，使得变换前后的电流的幅值都为1
• 先假设流入A相电流1A，则根据基尔霍夫电流定律，流出B相、C相的电流为-1/2A
• 求得Iα为3/2

$$\left[\begin{array}{c}{I}_{\alpha }=\frac{3}{2}\\ I_{\beta }=0\end{array}\right]=\left[\begin{array}{ccc}\cos 0\mathrm{°}& \cos 120\mathrm{°}& \cos 240\mathrm{°}\\ \sin 0\mathrm{°}& \sin 120\mathrm{°}& \sin 240\mathrm{°}\end{array}\right]\left[\begin{array}{c}{i}_a=1\\ i_b=-\frac{1}{2}\\ i_c=-\frac{1}{2}\end{array}\right]$$

• 为了让幅值相同，所以等式右边乘上一个2/3

$$\left[\begin{array}{c}{I}_{\alpha }=1\\ I_{\beta }=0\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}\cos 0\mathrm{°}& \cos 120\mathrm{°}& \cos 240\mathrm{°}\\ \sin 0\mathrm{°}& \sin 120\mathrm{°}& \sin 240\mathrm{°}\end{array}\right]\left[\begin{array}{c}{i}_a=1\\ i_b=-\frac{1}{2}\\ i_c=-\frac{1}{2}\end{array}\right]$$

• 所以得到克拉克变换的 等幅值形式 ：

$$\begin{gathered} \left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}\cos 0\mathrm{°}& \cos 120\mathrm{°}& \cos 240\mathrm{°}\\ \sin 0\mathrm{°}& \sin 120\mathrm{°}& \sin 240\mathrm{°}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right] \\ \left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right] \end{gathered}$$

等幅值形式的化简

通过观察可以发现，等幅值形式就是在基本形式的基础上乘上一个系数，所以这里直接在化简后的基本形式的基础上修改。

$$\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]=\frac{2}{3}\left[\begin{array}{cc}\frac{3}{2}& 0\\ \frac{\sqrt{3}}{2}& \sqrt{3}\end{array}\right]\left[\begin{array}{c}{i}_a\\ i_b\end{array}\right]$$

等幅值形式的逆运算

$$\begin{array}{rl}\left[\begin{array}{c}{i}_a\\ i_b\end{array}\right]& =\frac{3}{2}\left[\begin{array}{cc}\frac{2}{3}& 0\\ -\frac{1}{3}& \frac{\sqrt{3}}{3}\end{array}\right]\left[\begin{array}{c}{I}_{\alpha }\\ I_{\beta }\end{array}\right]\\ i_c& =-\frac{3}{2}(i_a+i_b)\end{array}$$

等功率形式

等功率形式就是在基本形式的基础上乘上$\sqrt{\frac{2}{3}}$

等功率形式的推导

等功率形式的化简

等功率形式的逆运算