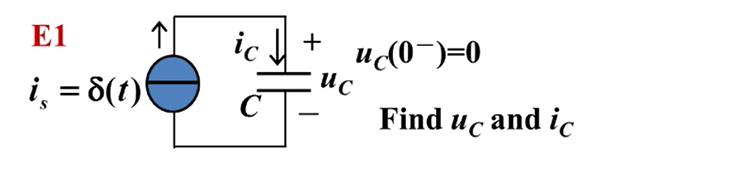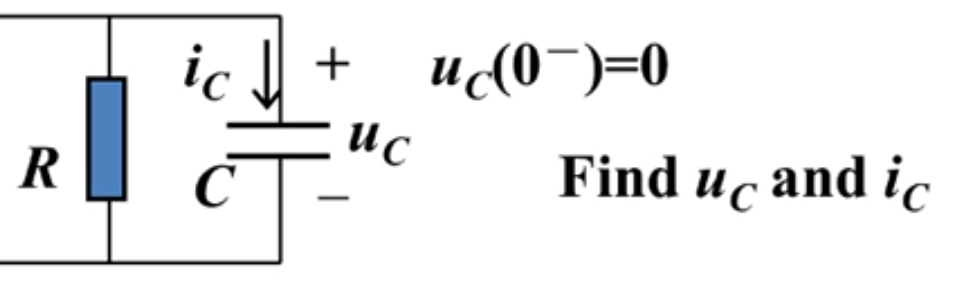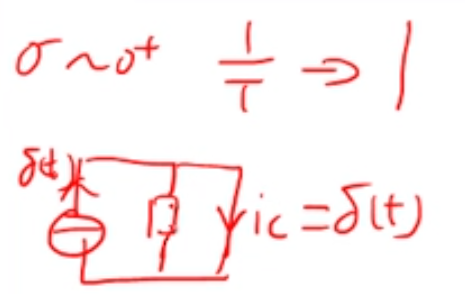单位冲激响应: 电路在单位冲激函数作用下的零状态响应ZSR
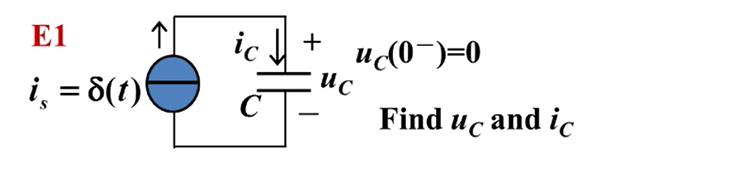
列写微分方程,两边求的积分。
- 拓扑约束KCL:
- 元件约束:
对于
所以有:
注:单位冲激函数的作用是将单位正电荷移动到电容上。
观察法
在零状态下,=0,如果不含冲击,则等于0,否则不为0.
对于更为复杂的电路,不能一眼看出中包含单位冲击函数的作用时,可以使用假设检验法:
假设没有冲击,则,相当于0值电压源或者导线:

- 通过观察可以发现,假设不成立。
所以:
将单位阶跃响应求导,得到单位冲击响应。

推导:

1. 求零状态单位阶跃响应
- 激励为单位阶跃函数
- 零状态则储能元件初值为0
于是有:
注:
- c表示电容,s表示单位阶跃激励作用下的响应
2. 用单位阶跃响应求单位冲击响应
注:
- c表示电容,s表示单位阶跃激励作用下的响应
- c表示电容,h表示单位冲击激励作用下的响应
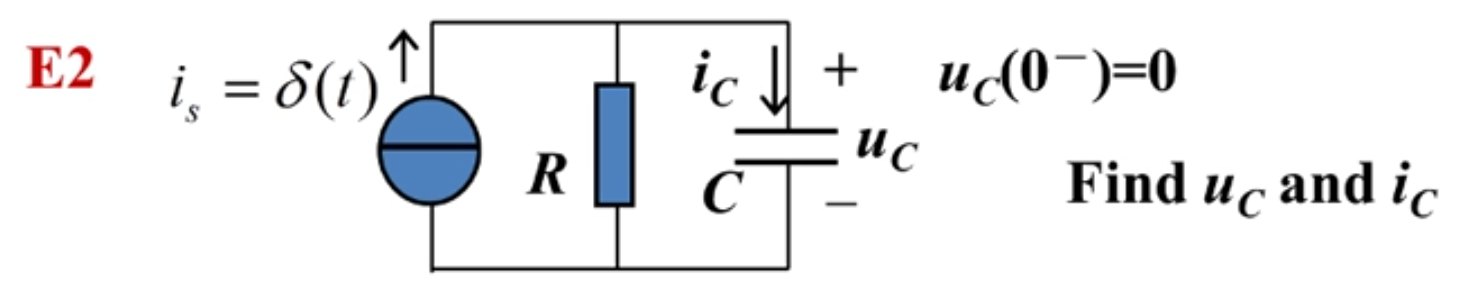
对于 t=0
注:可以理解为有界,而积分区间dt是无穷小,有界*无穷小=无穷小$,
另外,可以看出电流完全从电容流过,经过电阻的电流为0,因为电容电压不能突变,而电容初值为0,等效为0值电压源,即短路的导线。
对于 t>0
电流源看成开路
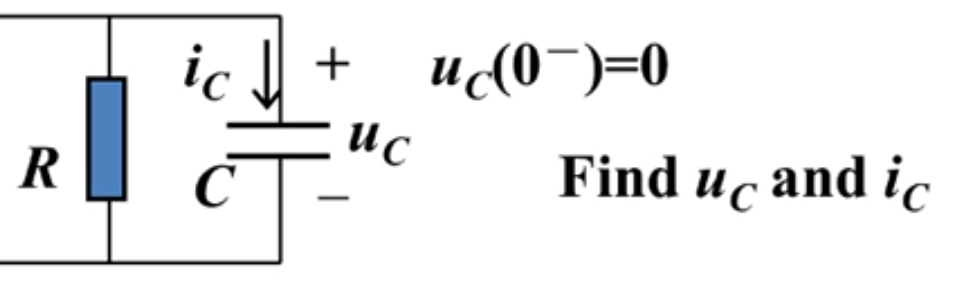
- 拓扑约束
- 元件约束
- 电容电压解三要素
- 时间常数:
- 初值:
- 稳态:
- 电容电流解三要素
- 时间常数:
- 初值:
- 稳态:
对于 t=0
假设即在电容电压保持不变,
那么电容始终等效为0值电压源,即导线。则:
- 假设: 则
- 检验:
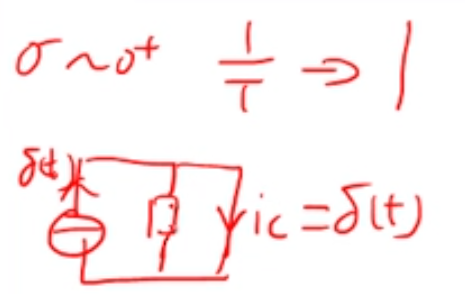
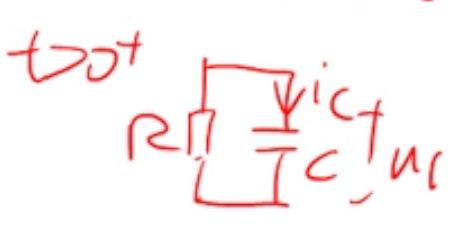
对于 t>0
按三要素法分析....
先求单位阶跃响应
- 拓扑约束
- 元件约束
- 电容电流解三要素
- 时间常数:
- 初值:
- 稳态:
- 电容电压解三要素
- 时间常数:
- 初值:
- 稳态:
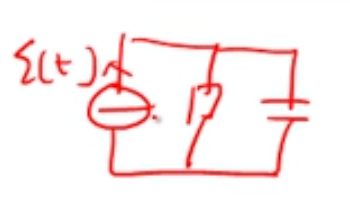
对单位阶跃响应s(t)求导得到单位冲击响应h(t)
- 求导过程中需要带着 因为是对全时域求导
- 求导经常要用到公式
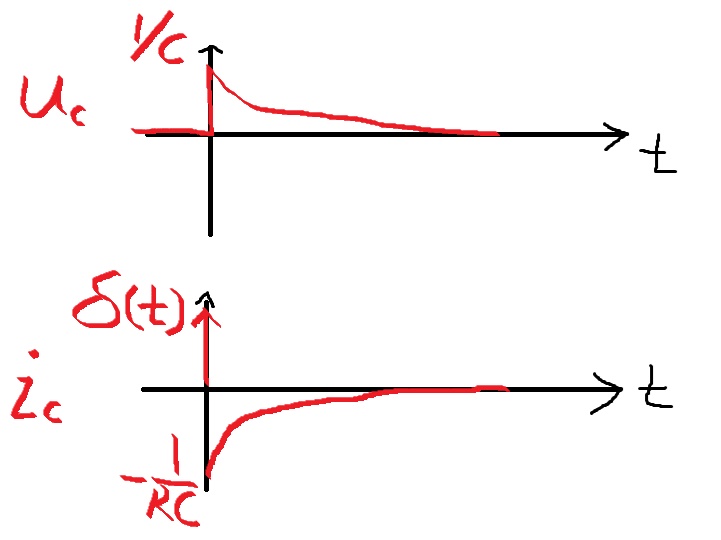
将方法三的计算结果和函数图像和方法一的对比,可以发现是完全一致的。