任意激励下的时域分析(A4)
2025/7/28大约 3 分钟
任意激励下的时域分析(卷积积分)
零状态(ZSR)条件的重要性质
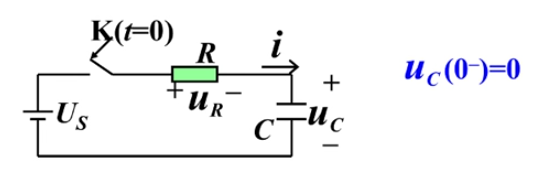
零状态条件的意义在于使得电路的激励和响应之间满足线性关系,从而满足齐次性和可加性。
卷积积分的概念
对于这个任意激励作用下的零状态电路,
由于是零状态,于是激励和响应必然满足线性关系,那么激励和响应必然满足齐次性和可加性。
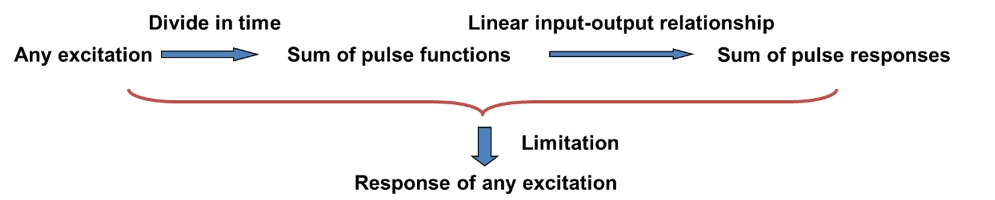
由于可加性,可以将任意激励在时间轴做划分,把激励看成是多个脉冲函数的和,于是响应就是这些脉冲函数单独作用的和。
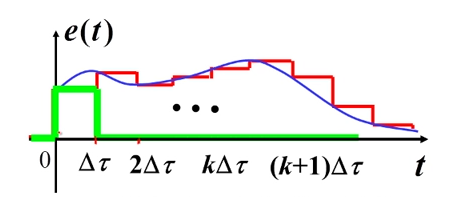
划分的时间单位越小,计算精度越高,取极限,就是卷积积分。
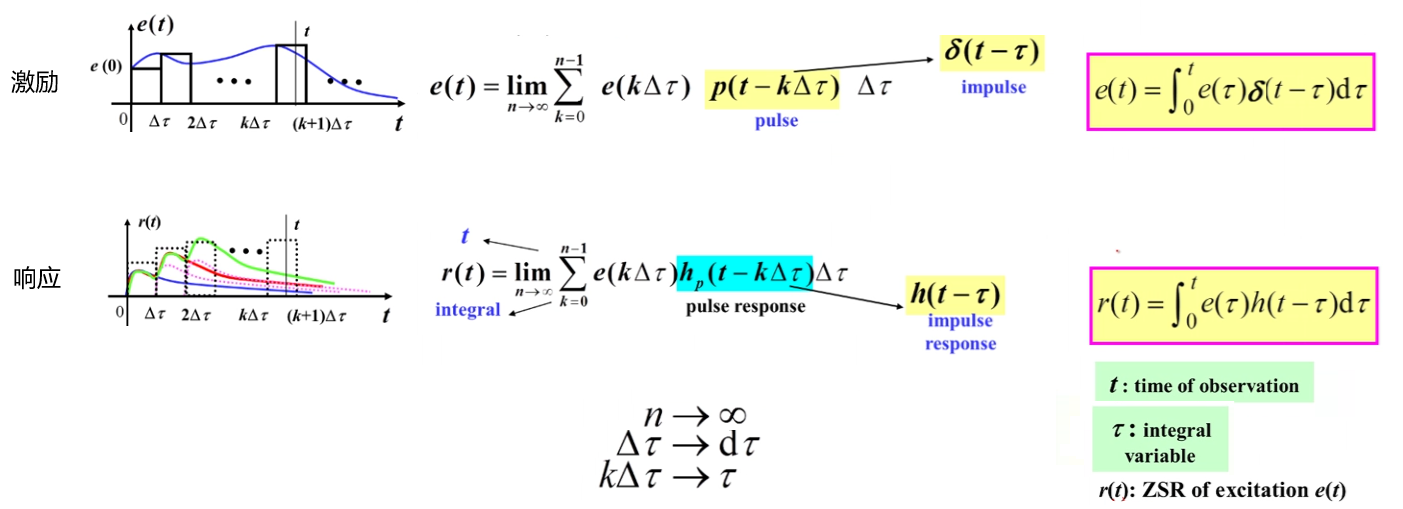
卷积积分的推导
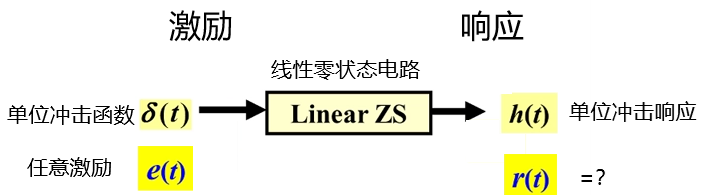
对于线性零状态电路,已知激励为单位冲击函数
那么只要能把任意激励函数
根据齐次性和可加性,响应
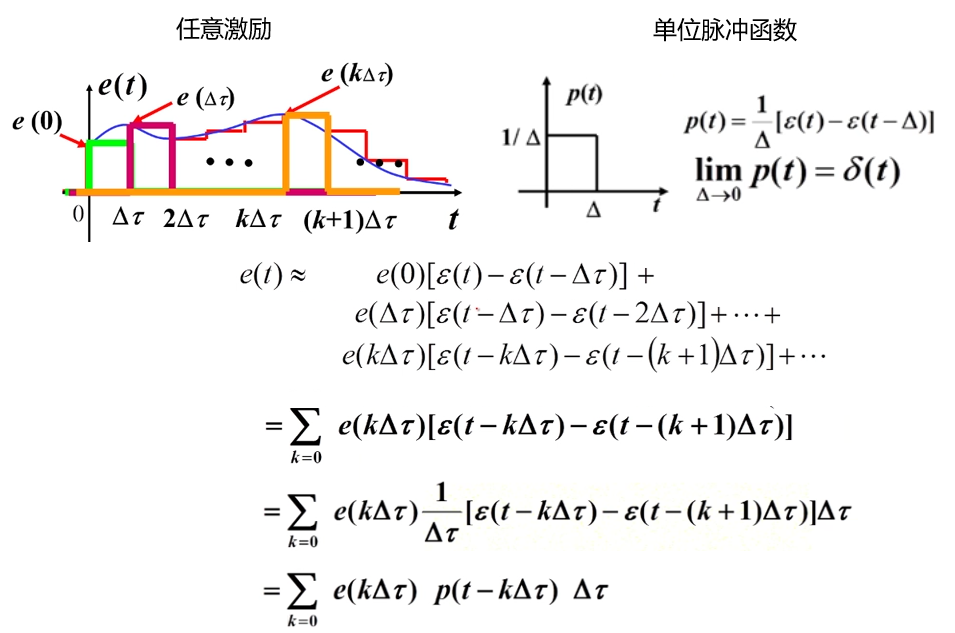
第一步,先把任意激励函数写成单位脉冲函数的形式。
第二步,利用齐次性,分析每个单位脉冲激励的响应。
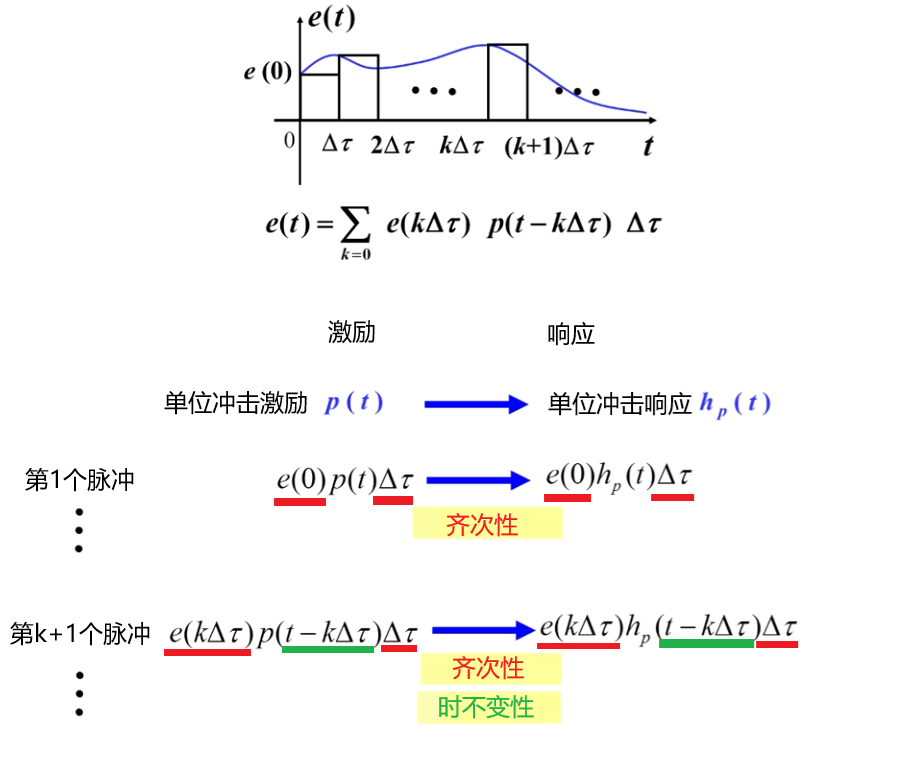
第三步,利用可加性,分析t时刻的响应
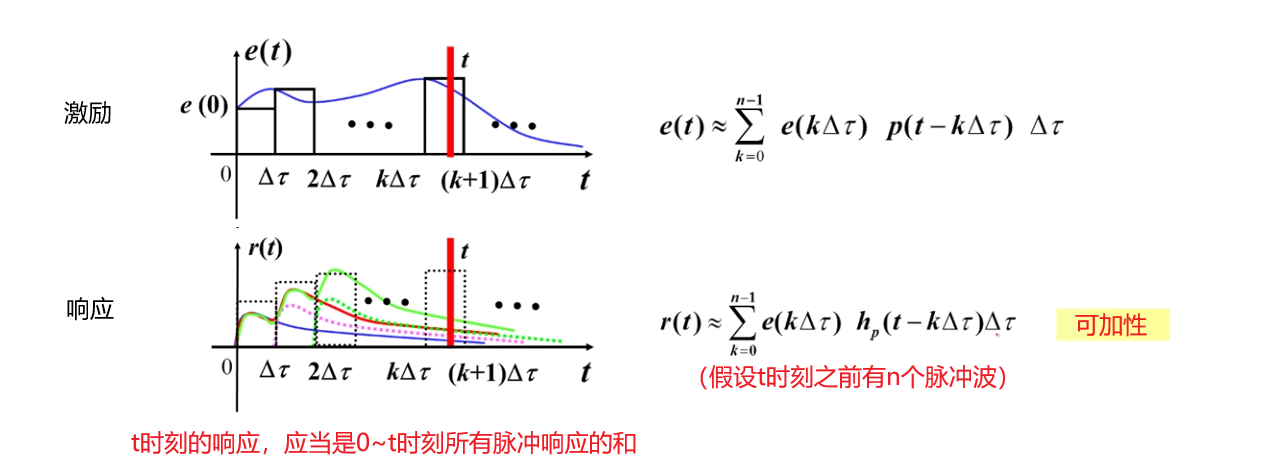
第四步,对激励和响应求极限,得到卷积积分
卷积积分的四个结论
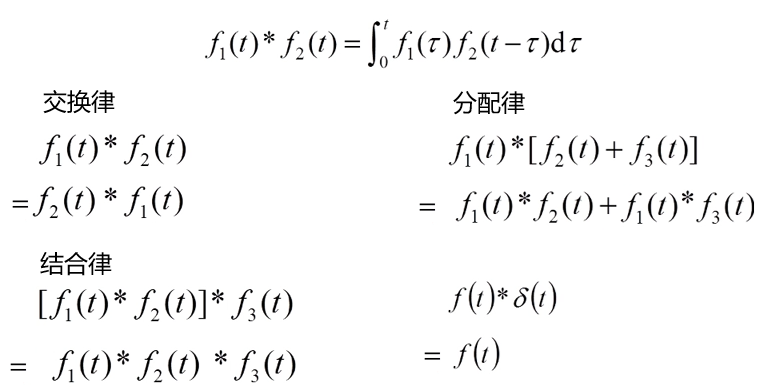
例题
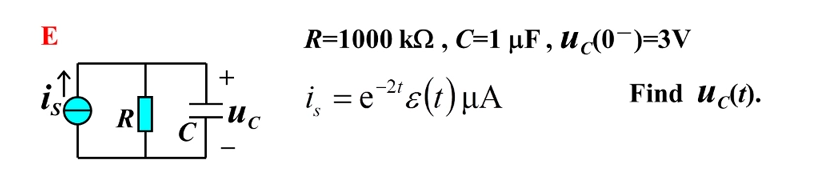
- 把电路的响应拆分为零输入响应+零状态响应
- 求解四部曲:
- ①求 ZIR,零输入响应
- 求零状态响应
- ②求
- ③求 ZSR=
- ②求
- ④求 FS全响应,FS=ZIR+ZSR
① 求ZIR
- 零输入,独立源不作用,储能元件作用;电流源看成开路,整个电路变成RC一阶电路。
②求
零状态,独立源作用,储能元件不作用,储能元件初值为0。
t=0
- 零状态电容看成0值电压源即导线
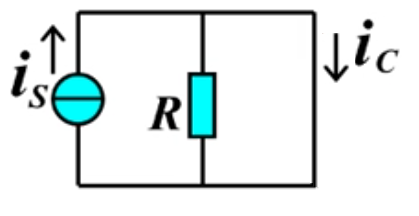
- 换路后电容有初值,看成RC电路
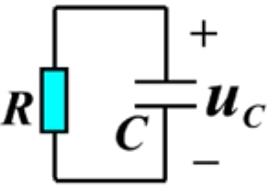
③求 ZSR=
④求 FS全响应,FS=ZIR+ZSR